44 физические приложения определенного интеграла inurl livre. Учебник. Геометрические приложения определенного интеграла. Объем тела вращения
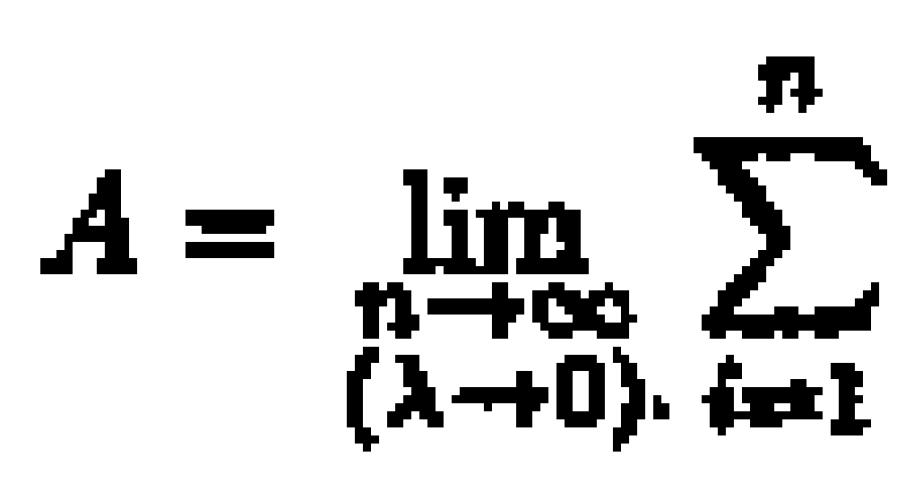
Читайте также
41.1. Схемы применения определенного интеграла
Пусть требуется найти значение какой-либо геометрической или физической величины А (площадь фигуры, объем тела, давление жидкости на вертикальную пластину и т. д.), связанной с отрезком изменения независимой переменной х. Предполагается, что эта величина А аддитивна, т. е. такая, что при разбиении отрезка [а; b] точкой с є (а; b) на части [а; с] и [с; b] значение величины А, соответствующее всему отрезку [а; b], равно сумме ее значений, соответствующих [а; с] и [с; b].
Для нахождения этой величины А можно руководствоваться одной из двух схем: I схема (или метод интегральных сумм) и II схема (или метод дифференциала).
Первая схема базируется на определении определенного интеграла.
1. Точками х 0 = а, x 1 ,..., x n = b разбить отрезок [а;b] на n частей. В соответствии с этим, интересующая нас величина А разобьется на n «элементарных слагаемых» ΔAi (i = 1,...,n): А = ΔA 1 +ΔА 2 +...+ ΔА n .
2. Представить каждое «элементарное слагаемое» в виде произведения некоторой функции (определяемой из условия задачи), вычисленной в произвольной точке соответствующего отрезка на его длину: ΔA i ≈ ƒ(c i)Δx i.
При нахождении приближенного значения ΔА i допустимы некоторые упрощения: дугу на малом участке можно заменить хордой, стягивающей ее концы; переменную скорость на малом участке можно приближенно считать постоянной и т. д.
Получим приближенное значение величины А в виде интегральной суммы:
3. Искомая величина А равна пределу интегральной суммы, т. е.

Указанный «метод сумм», как видим, основан на представлении интеграла как о сумме бесконечно большого числа бесконечно малых слагаемых.
Схема I была применена для выяснения геометрического и физического смысла определенного интеграла.
Вторая схема представляет собой несколько видоизмененную схему I и называется «метод дифференциала» или «метод отбрасывания бесконечно малых высших порядков»:
1) на отрезке [а;b] выбираем произвольное значение х и рассматриваем переменный отрезок [а; х]. На этом отрезке величина А становится функцией х: А = А(х), т. е. считаем, что часть искомой величины А есть неизвестная функция А(х), где х є - один из параметров величины А;
2) находим главную часть приращения ΔА при изменении х на малую величину Δх = dx, т. е. находим дифференциал dA функции А = А(х): dA = ƒ(х) dx, где ƒ(х), определяемая из условия задачи, функция переменной х (здесь также возможны различные упрощения);
3) считая, что dA ≈ ΔА при Δх → 0, находим искомую величину путем интегрирования dA в пределах от а до b:

41.2. Вычисление площадей плоских фигур
Прямоугольные координаты
Как уже было установлено (см. «геометрический смысл определенного интеграла»), площадь криволинейной трапеции, расположенной «выше» оси абсцисс (ƒ(х) ≥ 0), равна соответствующему определенному интегралу:


Формула (41.1) получена путем применения схемы I - метода сумм. Обоснуем формулу (41.1), используя схему II. Пусть криволинейная трапеция ограничена линиями у = ƒ(х) ≥ 0, х = а, х = b, у = 0 (см. рис. 174).
Для нахождения площади S этой трапеции проделаем следующие операции:
1. Возьмем произвольное х Î [а; b] и будем считать, что S = S(x).
2. Дадим аргументу х приращение Δх = dx (х + Δх є [а; b]). Функция S = S(x) получит приращение ΔS, представляющее собой площадь «элементарной криволинейной трапеции» (на рисунке она выделена).
Дифференциал площади dS есть главная часть приращения ΔS при Δх → 0, и, очевидно, он равен площади прямоугольника с основанием dx и высотой у: dS = у dx.
3. Интегрируя полученное равенство в пределах от х = а до х = b,получаем
Отметим,что если криволинейная трапеция расположена «ниже» оси Ох (ƒ(х) < 0), то ее площадь может быть найдена по формуле


Формулы (41.1)и (41.2) можно объединить в одну:

Площадь фигуры, ограниченной кривыми у = = fι(x) и у = ƒг(х), прямыми х = а и х = b (при условии ƒ 2 (х) ≥ ƒ 1 (х)) (см. рис. 175), можно найти по формуле
Если плоская фигура имеет «сложную» форму (см. рис. 176), то прямыми, параллельными оси Оу, ее следует разбить на части так, чтобы можно было бы применить уже известные формулы.

Если криволинейная трапеция ограничена прямыми у = с и у=d, осью Оу и
непрерывной кривой х = φ(у) ≥ 0 (см. рис. 177), то ее площадьнаходится по формуле
 И, наконец, если
криволинейная трапеция ограничена кривой, заданной параметрически
И, наконец, если
криволинейная трапеция ограничена кривой, заданной параметрически

прямыми х = аих = bи осью Ох, то площадь ее находится по формуле

где а и β определяютсяиз равенств х(а) = а и х(β) =b.
Пример 41.1 . Найти площадь фигуры, ограниченной осью Ох и графиком функции у = х 2 - 2х при х є .
Решение: Фигура имеет вид, изображенный на рисунке 178. Находим ее площадь S:

Пример 41.2. Вычислить площадь фигуры, ограниченной эллипсом х = а cos t, у = b sin t.
Решение: Найдем сначала 1/4 площади S. Здесь х изменяется от 0 до а, следовательно, t изменяется от до 0 (см. рис. 179). Находим:


Таким образом . Значит, S = π аВ.
Полярные координаты
Найдем площадь S криволинейного сектора, т. е. плоской фигуры, ограниченной непрерывной линией r=r(φ) и двумя лучами φ=а и φ=β (а < β), где r и φ - полярные координаты (см. рис. 180). Для решения задачи используем схему II - метод дифференциала.
 1. Будем считать часть
искомой площади S как функцию угла φ, т. е. S = S(φ), где а
≤
φ≤
β
(если φ = а, то S(a) = 0, если φ=β, то S(β) = S).
1. Будем считать часть
искомой площади S как функцию угла φ, т. е. S = S(φ), где а
≤
φ≤
β
(если φ = а, то S(a) = 0, если φ=β, то S(β) = S).
2. Если текущий полярный угол φ получит приращение Δφ = dφ, то приращение площади AS равно площади «элементарного криволинейного сектора» OAB.
Дифференциал dS представляет собой главную часть приращения ΔS при dφ→
0
и равен площади кругового сектора О АС (на рисунке она заштрихована)
радиуса r с центральным углом dφ. Поэтому![]()
3. Интегрируя полученное равенство в пределах от φ = а до φ = β, получим искомую площадь

Пример 41.3. Найти площадь фигуры, ограниченной «трехлепесткoвой розой» r=acos3φ (см. рис. 181).
Решение: Найдем сначала площадь половины одного лепестка «розы», т. е.1/6 часть всей площади фигуры:

т. е.. Следовательно,

Если плоская фигура имеет «сложную» форму, то лучами, выходящими из полюса, ее следует разбить на криволинейные секторы, к которым применить полученную формулу для нахождения площади. Так, для фигуры, изображенной на рисунке 182, имеем:

41.3. Вычисление длины дуги плоской кривой
Прямоугольные координаты
Пусть в прямоугольных координатах дана плоская кривая АВ, уравнение которой у=ƒ(х), где а≤х≤ b.
Под длиной дуги АВ понимается предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремится к нулю. Покажем, что если функция у=ƒ(х) и ее производная у" = ƒ"(х) непрерывны на отрезке [а; b], то кривая АВ имеет длину, равную


Применим схему I (метод сумм).
1. Точками х 0 = а, х 1 ..., х n = b (х 0 < x 1 < ...< х n) разобьем отрезок [а; b] на n частей (см. рис. 183). Пустьэтим точкам соответствуют точки М 0 = А, M 1 ,...,M n =В накривой АВ. Проведем хорды М 0 M 1 , M 1 M 2 ,..., М n-1 М n , длины которых обозначим соответственно через ΔL 1 , AL 2 ,..., ΔL n . Получим ломаную M 0 M 1 M 2 ... M n-ι M n , длина которой равна L n =ΔL 1 + ΔL 2 +...+ ΔL n =
2. Длину хорды (или звена ломаной) ΔL 1 можно найти по теореме Пифагора из треугольника с катетами Δx i и Δу i:
По теореме Лагранжа о конечном приращении функции Δу i =ƒ"(с i) Δх i , где ci є (x i-1 ;x i). Поэтому
а длина всей ломаной M 0 M 1 ... М n равна
3.Длина l кривой АВ, по определению, равна
![]()
![]() .
.
Заметим, что при ΔL i →
0
также и Δx i →
0
ΔLi =![]() и, следовательно,
|Δx i |<ΔL i).
и, следовательно,
|Δx i |<ΔL i).
Функция![]() непрерывна на отрезке [а; b], так как, по условию, непрерывна функция
ƒ"(х). Следовательно, существует предел интегральной суммы (41.4), когда max
Δx i →
0
:
непрерывна на отрезке [а; b], так как, по условию, непрерывна функция
ƒ"(х). Следовательно, существует предел интегральной суммы (41.4), когда max
Δx i →
0
:
Таким образом, или в
сокращенной записи l
=
или в
сокращенной записи l
=
Еслиуравнение кривой АВ задано в параметрической форме

где x(t) и y(t) - непрерывныефункции с непрерывными производными и х(а) = а, х(β) = b, то длина l кривой АВ находится по формуле

Формула (41.5) может быть получена из формулы (41.3) подстановкой x =
x(t),dx = x"(t)dt,![]()
Пример 41.4. Найти длину окружности радиуса R.
Решение: Найдем 1/4
часть ее длины от точки (0;R)до точки (R;0) (см. рис. 184). Так как
![]() то
то
Значит, l = 2π R. Если уравнение окружности записать в параметрическом виде х=Rcost, у = Rsint (0≤t≤2π ), то
Вычисление длины дуги может быть основано на применении метода дифференциала. Покажем, как можно получить формулу (41.3), применив схему II (метод дифференциала).
1. Возьмем произвольное значение х є [а; b] и рассмотрим переменный отрезок [а;х]. На нем величина l становится функцией от х, т.е. l = l (х) (l (а) = 0 и l (b) = l ).
 2. Находим дифференциал
dl
функции l
= l
(х) при изменении х на малую величину
Δх = dx: dl
= l
"(x)dx. Найдем l
"(x), заменяя бесконечномалую дугу MN хордой Δl
, стягивающей эту дугу(см. рис. 185):
2. Находим дифференциал
dl
функции l
= l
(х) при изменении х на малую величину
Δх = dx: dl
= l
"(x)dx. Найдем l
"(x), заменяя бесконечномалую дугу MN хордой Δl
, стягивающей эту дугу(см. рис. 185):

 3. Интегрируя dl в
пределах от а до b, получаем
3. Интегрируя dl в
пределах от а до b, получаем
Равенство![]() называетсяформулой дифференциала дуги в прямоугольных координатах.
называетсяформулой дифференциала дуги в прямоугольных координатах.
Так как у" х = -dy/dx, то
![]()
Последняя формула представляет собой теорему Пифагора для бесконечно малого треугольника МСТ (см. рис. 186).
Полярные координаты
Пусть кривая АВ задана уравнением в полярных координатах r = r(φ), а≤φ≤β. Предположим, что r(φ) и r"(φ) непрерывны на отрезке [а;β].
Если в равенствах х = rcosφ, у = rsinφ, связывающих полярные и декартовы координаты, параметром считать угол φ, то кривую АВ можнозадать параметрически



Применяя формулу (41.5), получаем

Пример 41.5. Найти длину кардиоиды r = = а(1 + cosφ).
 Решение: Кардиоида r =
а(1 + cosφ) имеет вид, изображенный на рисунке 187. Она симметрична
относительно полярной оси. Найдем половину длины кардиоиды:
Решение: Кардиоида r =
а(1 + cosφ) имеет вид, изображенный на рисунке 187. Она симметрична
относительно полярной оси. Найдем половину длины кардиоиды:

Таким образом, 1/2l= 4а. Значит, l= 8а.
41.4. Вычисление объема тела
Вычисление объема тела по известным площадям параллельных сечений
Пусть требуется найти объем V тела, причем известны площади S сечений этого тела плоскостями, перпендикулярными некоторой оси, например оси Ох: S = S(x), а ≤ х ≤ b.
 1. Через произвольную
точку х є проведем плоскость ∏, перпендикулярную оси Ох (см. рис.
188). Обозначим через S(x) площадь сечения тела этой плоскостью; S(x)
считаем известной и непрерывно изменяющейся при изменении х. Через v(x)
обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на
отрезке [а; х] величина v есть функция от х, т. е. v = v(x)
(v(a) = 0, v(b) = V).
1. Через произвольную
точку х є проведем плоскость ∏, перпендикулярную оси Ох (см. рис.
188). Обозначим через S(x) площадь сечения тела этой плоскостью; S(x)
считаем известной и непрерывно изменяющейся при изменении х. Через v(x)
обозначим объем части тела, лежащее левее плоскости П. Будем считать, что на
отрезке [а; х] величина v есть функция от х, т. е. v = v(x)
(v(a) = 0, v(b) = V).
2. Находим дифференциал dV функции v = v(x). Он представляет собой «элементарный слой» тела, заключенный между параллельными плоскостями, пересекающими ось Ох в точках х и х+Δх, который приближенно может быть принят за цилиндр с основанием S(x) и высотой dx. Поэтому дифференциал объема dV = S(x) dx.
3. Находим искомую величину V путем интегрирования dA в пределах от а до В:

Полученная формула называется формулой объема тела по площади параллельных сечений.
Пример 41
.6. Найти объем эллипсоида
 Решение: Рассекая
эллипсоид плоскостью, параллельной плоскости Oyz и на расстоянии х от нее
(-а≤х≤
a), получим эллипс
(см. рис. 189):
Решение: Рассекая
эллипсоид плоскостью, параллельной плоскости Oyz и на расстоянии х от нее
(-а≤х≤
a), получим эллипс
(см. рис. 189):

Площадь этого эллипса равна![]()
Поэтому, поформуле (41.6), имеем

Объем тела вращения
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией у = ƒ(х) 0, отрезком а ≤ x ≤ bи прямыми х = а и х = b (см. рис. 190). Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох (х Î [а; b]), есть круг с радиусом у= ƒ(х). Следовательно, S(x)=π y 2.
 Применяя формулу (41.6)
объема тела по площади параллельных сечений, получаем
Применяя формулу (41.6)
объема тела по площади параллельных сечений, получаем

Если криволинейная трапеция ограничена графиком не прерывной функциих=φ(у) ≥ 0 и прямыми х = 0, у = с,
у = d (с < d), то объем тела, образованного вращением этой трапеции вокруг оси Оу, по аналогии с формулой (41.7), равен

 Пример 41.7. Найти
объем тела, образованного вращением фигуры, ограниченной линиямивокруг
оси Оу (см. рис. 191).
Пример 41.7. Найти
объем тела, образованного вращением фигуры, ограниченной линиямивокруг
оси Оу (см. рис. 191).
Решение:По формуле (41.8) находим:

41.5. Вычисление площади поверхности вращения
Пусть кривая АВ является графиком функции у = ƒ(х) ≥ 0, где х є [а;b], а функция у = ƒ(х) и ее производная у"=ƒ"(х) непрерывны на этом отрезке.
Найдем площадь S поверхности, образованной вращением кривой АВ вокруг оси Ох.
Применим схему II (метод дифференциала).
 1. Через произвольную
точку х є [а; b] проведем плоскость ∏, перпендикулярную оси Ох. Плоскость ∏
пересекает поверхность вращения по окружности с радиусом у = ƒ(х) (см. рис.
192). Величина S поверхности части фигуры вращения, лежащей левее плоскости,
является функцией от х, т. е. s=s(x) (s(a)=0 и s(b)=S).
1. Через произвольную
точку х є [а; b] проведем плоскость ∏, перпендикулярную оси Ох. Плоскость ∏
пересекает поверхность вращения по окружности с радиусом у = ƒ(х) (см. рис.
192). Величина S поверхности части фигуры вращения, лежащей левее плоскости,
является функцией от х, т. е. s=s(x) (s(a)=0 и s(b)=S).
2. Дадим аргументу х приращение Δх = dx. Через точку х + dx є [а; b] также проведем плоскость, перпендикулярную оси Ох. Функция s=s(x) получит приращение Аз, изображенного на рисунке в виде «пояска».
Найдем дифференциал площади ds, заменяя образованную между сечениями фигуру усеченным конусом, образующая которого равна dl , а радиусы оснований рав ны у и у+dy. Площадь его боковой поверхности равна ds=π (у+у+dy ) dl =2π уdl + π dydl . Отбрасывая произведение dydl как бесконечно малую высшего порядка, чем ds, получаем ds=2π уdl , или, так как
3. Интегрируя полученное равенство в пределах от х = а до х = b, получаем
Если кривая АВ задана параметрическими уравнениями х = x(t),y=y(t), t 1 ≤ t ≤ t 2 , то формула (41.9) для площади поверхности вращения принимает вид

Пример 41.8. Найти площадь поверхности шара радиуса R.

Пример 41.9. Дана циклоида

Найти площадь поверхности, образованной вращением ее вокруг оси Ох.
Решение: При вращении половины дуги циклоиды вокруг оси Ох площадь поверхности вращения равна

41.6. Механические приложения определенного интеграла
Работа переменной силы
Пусть материальная точка М перемещается вдоль оси Ох под действием переменной силы F = F(x), направленной параллельно этой оси. Работа, произведенная силой при перемещении точки М из положения х = а в положение х = b (a < b), находится по формуле (см. п. 36).
Пример 41.10 Какую работу нужно затратить, чтобы растянуть пружину на 0,05 м, если сила 100 Н растягивает пружину на 0,01 м?
Решение: По закону Гука упругая сила, растягивающая пружину, пропорциональна этому растяжению х, т. е. F = kх, где k - коэффициент пропорциональности. Согласно условию задачи, сила F = 100 Н растягивает пружину на х = 0,01 м; следовательно, 100 = k*0,01, откуда k = 10000; следовательно,F = 10000х.
Искомая работа на основании формулы (41.10) равна
Пример 41.11. Найти работу, которую необходимо затратить, чтобы выкачать через край жидкость из вертикального цилиндрического резервуара высоты Н м и радиусом основания R м.
Решение: Работа, затрачиваемая на поднятие тела весом р на высоту h, равна р h. Но различные слои жидкости в резервуаре находятся на различных глубинах и высота поднятия (до края резервуара) различных слоев не одинакова.
 Для решения поставленной
задачи применим схему II (метод дифференциала). Введем систему координат
так, как указано на рисунке 193.
Для решения поставленной
задачи применим схему II (метод дифференциала). Введем систему координат
так, как указано на рисунке 193.
1. Работа, затрачиваемая на выкачивание из резервуара слоя жидкости толщиной x (0 !!!< x !!!< H), есть функция от х, т.е. А = А(х), где 0≤x≤H (А(0)=0, А(Н)=А 0).
2. Находим главную часть приращения ΔА при изменении х на величину Δх = dx, т. е. находим дифференциал dA функции А(х).
Ввиду малости dx считаем, что «элементарный» слой жидкости находится на одной глубине х (от края резервуара) (см. рис. 193). Тогда dA = dp*x, где dp - вес этого слоя; он равен g *g dv, где g - ускорение свободного падения, g - плотность жидкости, dv - объем «элементарного» слоя жидкости (на рисунке он выделен), т. е. dp = gg dv. Объем указанного слоя жидкости, очевидно, равен π R 2 dx, где dx - высота цилиндра (слоя), π R 2 - площадь его основания, т. е. dv=π R 2 dx.
Таким образом, dp=gg π R 2 dx и dA = gg π R 2 dx*x.
3) Интегрируя полученное равенство в пределах от х = 0 до х = Н, находим

Путь, пройденный телом
Пусть материальная точка перемещается по прямой с переменной скоростью v=v(t). Найдем путь S, пройденный ею за промежуток времени от t 1 до t 2 .
Решение: Из физического смысла производной известно, что при движении
точки в одном направлении «скорость прямолинейного движения равна
производной от пути по времени», т. е..
Отсюда следует, что dS = v(t)dt. Интегрируя полученное равенство в пределах
от t 1 до t 2 , получаем

Отметим, что эту же формулу можно получить, пользуясь схемой I или II применения определенного интеграла.
Пример 41.12. Найти путь, пройденный телом за 4 секунды от начала движения, если скорость тела v(t) = 10t + 2 (м/с).
Решение: Если v(t)=10t+2 (м/с), то путь, пройденный телом от начала движения (t=0) до конца 4-й секунды, равен
Давление жидкости на вертикальную пластинку
По закону Паскаля давление жидкости на горизонтальную пластину равно весу столба этой жидкости, имеющего основанием пластинку, а высотой - глубину ее погружения от свободной поверхности жидкости, т. е. Р = g*g* S* h, где g - ускорение свободного падения, g - плотность жидкости, S - площадь пластинки, h - глубина ее погружения.
По этой формуле нельзя искать давление жидкости на вертикально погруженную пластинку, так как ее разные точки лежат на разных глубинах.
Пусть в жидкость погружена вертикально пластина, ограниченная линиями х = а, х = b, у 1 = f 1 (x) и у 2 =ƒ 2 (х); система координат выбрана так, как указано на рисунке 194. Для нахождения давления Р жидкости на эту пластину применим схему II (метод дифференциала).
 1. Пусть часть искомой
величины Р есть функция от х: р=р(х), т. е. р=р(х) - давление на часть
пластины, соответствующее отрезку [а; х] значений переменной х, где х є [а;
b] (р(а)=0,р(b) = Р).
1. Пусть часть искомой
величины Р есть функция от х: р=р(х), т. е. р=р(х) - давление на часть
пластины, соответствующее отрезку [а; х] значений переменной х, где х є [а;
b] (р(а)=0,р(b) = Р).
2. Дадим аргументу х приращение Δх = dx. Функция р(х) получит приращение Δр (на рисунке - полоска-слой толщины dx). Найдем дифференциал dp этой функции. Ввиду малости dx будем приближенно считать полоску прямоугольником, все точки которого находятся на одной глубине х, т. е. пластинка эта - горизонтальная.
Тогда по закону Паскаля

3. Интегрируя полученное равенство в пределах от х = а до х = В, получим
 Пример 41.13.
Определить величину давления воды на полукруг, вертикально погруженный в
жидкость, если его радиус R, а центр О находится на свободной поверхности
воды (см. рис. 195).
Пример 41.13.
Определить величину давления воды на полукруг, вертикально погруженный в
жидкость, если его радиус R, а центр О находится на свободной поверхности
воды (см. рис. 195).
Аналогично определяется статический момент S y этой системы
относительно оси ![]()
Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.
Пусть у = ƒ(х) (a≤ x≤ b) - это уравнение материальной кривой АВ. Будем считать ее однородной с постоянной линейной плотностью g (g = const).
Для произвольного х є [а; b] на кривой АВ найдется точка с координатами (х;у). Выделим на кривой элементарный участок длины dl, содержащий точку (х;у). Тогда масса этого участка равна g dl. Примем этот участок dl приближенно за точку, отстоящую от оси Ох на расстоянии у. Тогда дифференциал статического момента dS x («элементарный момент») будет равен g dly, т. е. dS x = g dlу (см. рис. 196).
 Отсюда следует, что
статический момент S x кривой АВ относительно оси Ох равен
Отсюда следует, что
статический момент S x кривой АВ относительно оси Ох равен

Аналогично находим S y:

Статические моменты S x и S y кривой позволяют легко установить положение ее центра тяжести (центра масс).
Центром тяжести материальной плоской кривой у = ƒ(х), х Î называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу m заданной кривой, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей кривой у = ƒ (х) относительно той же оси. Обозначим через С(х с;у с) центр тяжести кривой АВ.
Из определения центра тяжести следуют равенства![]() Отсюда
Отсюда
Вычисление статических моментов и координат центра тяжести плоской фигуры
Пусть дана материальная плоская фигура (пластинка), ограниченная кривой у = ƒ(х) 0 и прямыми у = 0, х = a, x = b (см. рис. 198).
 Будем считать, что
поверхностная плотность пластинки постоянна (g
=
const). Тогда масса «всей пластинки равна g
* S,
т. е
Будем считать, что
поверхностная плотность пластинки постоянна (g
=
const). Тогда масса «всей пластинки равна g
* S,
т. е Выделим элементарный
участок пластинки в виде бесконечно узкой вертикальной полосы и будем
приближенно считать его прямоугольником.
Выделим элементарный
участок пластинки в виде бесконечно узкой вертикальной полосы и будем
приближенно считать его прямоугольником.
Тогда масса его равна g ydx. Центр тяжести С пря моугольника лежит на пересечении диагоналей прямоугольника. Эта точка С отстоит от оси Ох на 1/2*у, а от оси Оу на х (приближенно; точнее на расстоянии х+ 1 / 2 ∆х). Тогда для элементарных статических моментов относительно осей Ох и Оу выполнены соотношения
Итак, центр тяжести имеет координаты
Определенный интеграл (ОИ) широко используется в практических приложениях математики и физики.
В частности, в геометрии с помощью ОИ находят площади простых фигур и сложных поверхностей, объемов тел вращения и тел произвольной формы, длин кривых на плоскости и в пространстве.
В физике и теоретической механике ОИ применяют для вычисления статических моментов, масс и центров масс материальных кривых и поверхностей, для вычисления работы переменной силы по криволинейному пути и др.
Площадь плоской фигуры
Пусть некоторая плоская фигура в декартовой прямоугольной системе координат $xOy$ сверху ограничена кривой $y=y_{1} \left(x\right)$, снизу -- кривой $y=y_{2} \left(x\right)$, а слева и справа вертикальными прямыми $x=a$ и $x=b$ соответственно. В общем случае площадь такой фигуры выражается с помощью ОИ $S=\int \limits _{a}^{b}\left(y_{1} \left(x\right)-y_{2} \left(x\right)\right)\cdot dx $.
Если же некоторая плоская фигура в декартовой прямоугольной системе координат $xOy$ справа ограничена кривой $x=x_{1} \left(y\right)$, слева -- кривой $x=x_{2} \left(y\right)$, а снизу и сверху горизонтальными прямыми $y=c$ и $y=d$ соответственно, то площадь такой фигуры выражается с помощью ОИ $S=\int \limits _{c}^{d}\left(x_{1} \left(y\right)-x_{2} \left(y\right)\right)\cdot dy $.
Пусть плоская фигура (криволинейный сектор), рассматриваемая в полярной системе координат, образована графиком непрерывной функции $\rho =\rho \left(\phi \right)$, а также двумя лучами, проходящими под углами $\phi =\alpha $ и $\phi =\beta $ соответственно. Формула для вычисления площади такого криволинейного сектора имеет вид: $S=\frac{1}{2} \cdot \int \limits _{\alpha }^{\beta }\rho ^{2} \left(\phi \right)\cdot d\phi $.
Длина дуги кривой
Если на отрезке $\left[\alpha ,\; \beta \right]$ кривая задана уравнением $\rho =\rho \left(\phi \right)$ в полярной системе координат, то длина её дуги вычисляется с помощью ОИ $L=\int \limits _{\alpha }^{\beta }\sqrt{\rho ^{2} \left(\phi \right)+\rho "^{2} \left(\phi \right)} \cdot d\phi $.
Если на отрезке $\left$ кривая задана уравнением $y=y\left(x\right)$, то длина её дуги вычисляется с помощью ОИ $L=\int \limits _{a}^{b}\sqrt{1+y"^{2} \left(x\right)} \cdot dx $.
Если на отрезке $\left[\alpha ,\; \beta \right]$ кривая задана параметрически, то есть $x=x\left(t\right)$, $y=y\left(t\right)$, то длина её дуги вычисляется с помощью ОИ $L=\int \limits _{\alpha }^{\beta }\sqrt{x"^{2} \left(t\right)+y"^{2} \left(t\right)} \cdot dt $.
Вычисление объема тела по площадям параллельных сечений
Пусть необходимо найти объем пространственного тела, координаты точек которого удовлетворяют условиям $a\le x\le b$, и для которого известны площади сечений $S\left(x\right)$ плоскостями, перпендикулярными оси $Ox$.
Формула для вычисления объема такого тела имеет вид $V=\int \limits _{a}^{b}S\left(x\right)\cdot dx $.
Объем тела вращения
Пусть на отрезке $\left$ задана неотрицательная непрерывная функция $y=y\left(x\right)$, образующая криволинейную трапецию (КрТ). Если вращать эту КрТ вокруг оси $Ox$, то образуется тело, называемое телом вращения.
Вычисление объема тела вращения является частным случаем вычисления объема тела по известным площадям его параллельных сечений. Соответствующая формула имеет вид $V=\int \limits _{a}^{b}S\left(x\right)\cdot dx =\pi \cdot \int \limits _{a}^{b}y^{2} \left(x\right)\cdot dx $.
Пусть некоторая плоская фигура в декартовой прямоугольной системе координат $xOy$ сверху ограничена кривой $y=y_{1} \left(x\right)$, снизу -- кривой $y=y_{2} \left(x\right)$, где $y_{1} \left(x\right)$ и $y_{2} \left(x\right)$ -- неотрицательные непрерывные функции, а слева и справа вертикальными прямыми $x=a$ и $x=b$ соответственно. Тогда объем тела, образованного вращением этой фигуры вокруг оси $Ox$, выражается ОИ $V=\pi \cdot \int \limits _{a}^{b}\left(y_{1}^{2} \left(x\right)-y_{2}^{2} \left(x\right)\right)\cdot dx $.
Пусть некоторая плоская фигура в декартовой прямоугольной системе координат $xOy$ справа ограничена кривой $x=x_{1} \left(y\right)$, слева -- кривой $x=x_{2} \left(y\right)$, где $x_{1} \left(y\right)$ и $x_{2} \left(y\right)$ -- неотрицательные непрерывные функции, а снизу и сверху горизонтальными прямыми $y=c$ и $y=d$ соответственно. Тогда объем тела, образованного вращением этой фигуры вокруг оси $Oy$, выражается ОИ $V=\pi \cdot \int \limits _{c}^{d}\left(x_{1}^{2} \left(y\right)-x_{2}^{2} \left(y\right)\right)\cdot dy $.
Площадь поверхности тела вращения
Пусть на отрезке $\left$ задана неотрицательная функция $y=y\left(x\right)$ с непрерывной производной $y"\left(x\right)$. Эта функция образует КрТ. Если вращать эту КрТ вокруг оси $Ox$, то она сама образует тело вращения, а дуга КрТ -- его поверхность. Площадь поверхности такого тела вращения выражается формулой $Q=2\cdot \pi \cdot \int \limits _{a}^{b}y\left(x\right)\cdot \sqrt{1+y"^{2} \left(x\right)} \cdot dx $.
Предположим, что кривую $x=\phi \left(y\right)$, где $\phi \left(y\right)$ -- заданная на отрезке $c\le y\le d$ неотрицательна функция, вращают вокруг оси $Oy$. В этом случае площадь поверхности образованного тела вращения выражается ОИ $Q=2\cdot \pi \cdot \int \limits _{c}^{d}\phi \left(y\right)\cdot \sqrt{1+\phi "^{2} \left(y\right)} \cdot dy $.
Физические приложения ОИ
- Для вычисления пройденного пути в момент времени $t=T$ при переменной скорости движения $v=v\left(t\right)$ материальной точки, которая начала движение в момент времени $t=t_{0} $, используют ОИ $S=\int \limits _{t_{0} }^{T}v\left(t\right)\cdot dt $.
- Для вычисления работы переменной сили $F=F\left(x\right)$, приложенной к материальной точке, перемещающейся по прямолинейному пути вдоль оси $Ox$ от точки $x=a$ до точки $x=b$ (направление действия силы совпадает с направлением движения) используют ОИ $A=\int \limits _{a}^{b}F\left(x\right)\cdot dx $.
- Статические моменты относительно координатных осей материальной кривой $y=y\left(x\right)$ на промежутке $\left$ выражаются формулами $M_{x} =\rho \cdot \int \limits _{a}^{b}y\left(x\right)\cdot \sqrt{1+y"^{2} \left(x\right)} \cdot dx $ и $M_{y} =\rho \cdot \int \limits _{a}^{b}x\cdot \sqrt{1+y"^{2} \left(x\right)} \cdot dx $, где линейная плотность $\rho $ этой кривой считается постоянной.
- Центр масс материальной кривой -- это точка, в которой условно сосредоточена вся её масса таким образом, что статические моменты точки относительно координатных осей равны соответствующим статическим моментам всей кривой в целом.
- Статические моменты материальной плоской фигуры в виде КрТ относительно координатных осей выражаются формулами $M_{x} =\frac{1}{2} \cdot \rho \cdot \int \limits _{a}^{b}y^{2} \left(x\right)\cdot dx $ и $M_{y} =\rho \cdot \int \limits _{a}^{b}x\cdot y\left(x\right)\cdot dx $.
- Координаты центра масс материальной плоской фигуры в виде КрТ, образованной кривой $y=y\left(x\right)$ на промежутке $\left$, вычисляют по формулам $x_{C} =\frac{\int \limits _{a}^{b}x\cdot y\left(x\right)\cdot dx }{\int \limits _{a}^{b}y\left(x\right)\cdot dx } $ и $y_{C} =\frac{\frac{1}{2} \cdot \int \limits _{a}^{b}y^{2} \left(x\right)\cdot dx }{\int \limits _{a}^{b}y\left(x\right)\cdot dx } $.
Формулы для вычисления координат центра масс плоской кривой имеют вид $x_{C} =\frac{\int \limits _{a}^{b}x\cdot \sqrt{1+y"^{2} \left(x\right)} \cdot dx }{\int \limits _{a}^{b}\sqrt{1+y"^{2} \left(x\right)} \cdot dx } $ и $y_{C} =\frac{\int \limits _{a}^{b}y\left(x\right)\cdot \sqrt{1+y"^{2} \left(x\right)} \cdot dx }{\int \limits _{a}^{b}\sqrt{1+y"^{2} \left(x\right)} \cdot dx } $.
1. Площадь плоской фигуры.
Площадь криволинейной трапеции, ограниченной неотрицательной функцией f (x) , осью абсцисс и прямыми x = a , x = b , определяется как S = ∫ a b f x d x .
Площадь криволинейной трапеции
Площадь фигуры, ограниченной функцией f (x) , пересекающей ось абсцисс, определяется формулой S = ∑ i: f x ≥ 0 ∫ x i - 1 x i f x d x - ∑ i: f x < 0 ∫ x i - 1 x i | f x | d x , где x i – нули функции. Другими словами, чтобы вычислить площадь этой фигуры, нужно разбить отрезок нулями функции f (x) на части, проинтегрировать функцию f по каждому из получившихся промежутков знакопостоянства, сложить отдельно интегралы по отрезкам, на которых функция f принимает разные знаки, и вычесть из первого второе.
2. Площадь криволинейного сектора.
Площадь криволинейного сектора Рассмотрим кривую ρ = ρ (φ) в полярной системе координат, где ρ (φ) – непрерывная и неотрицательная на [α; β] функция. Фигура, ограниченная кривой ρ (φ) и лучами φ = α , φ = β , называется криволинейным сектором. Площадь криволинейного сектора равна S = 1 2 ∫ α β ρ 2 φ d φ .
3. Объем тела вращения.
Объем тела вращения
Пусть тело образовано вращением вокруг оси OX криволинейной трапеции, ограниченной непрерывной на отрезке функцией f (x) . Его объем выражается формулой V = π ∫ a b f 2 x d x .
 К задаче о нахождении объема тела по площади поперечного сечения
К задаче о нахождении объема тела по площади поперечного сечения
Пусть тело заключено между плоскостями x = a и x = b , а площадь его сечения плоскостью, проходящей через точку x , – непрерывная на отрезке функция σ (x) . Тогда его объем равен V = ∫ a b σ x d x .
4. Длина дуги кривой.
Пусть задана кривая r → t = x t , y t , z t Тогда длина ее участка, ограниченного значениями t = α и t = β выражается формулой S = ∫ α β x ′ t 2 + y ′ t 2 + z ′ t 2 dt .
 Длина дуги плоской кривой
В частности, длина плоской кривой, задаваемой на координатной плоскости OXY
уравнением y = f (x)
, a ≤ x ≤ b
, выражается формулой
S =
∫
a
b
1 +
f
′
x
2
dx
.
Длина дуги плоской кривой
В частности, длина плоской кривой, задаваемой на координатной плоскости OXY
уравнением y = f (x)
, a ≤ x ≤ b
, выражается формулой
S =
∫
a
b
1 +
f
′
x
2
dx
.
5. Площадь поверхности вращения.
Площадь поверхности вращения Пусть поверхность задается вращением относительно оси OX графика функции y = f (x) , a ≤ x ≤ b , и функция f имеет непрерывную производную на этом отрезке. Тогда площадь поверхности вращения определяется формулой Π = 2 π ∫ a b f x 1 + f ′ x 2 d x .
Тема 6.10. Геометрические и физические приложения определенного интеграла
1. Площадь криволинейной трапеции, ограниченной кривой y =f(x)(f(x)>0), прямыми x = a , x = b и отрезком [ a , b ] оси Ох, вычисляется по формуле
2. Площадь фигуры, ограниченной кривыми y = f (x) и y = g (x) (f (x)< g (x)) и прямыми х= a , x = b , находится по формуле
3. Если кривая задана параметрическими уравнениями x = x (t), y = y (t), то площадь криволинейной трапеции, ограниченной этой кривой и прямыми х=a , x= b , находится по формуле
4. Пусть S (x)- площадь сечения тела плоскостью, перпендикулярной оси Ох, тогда объем части тела, заключенной между перпендикулярными оси плоскостями х=а и х= b , находится по формуле
5. Пусть криволинейная трапеция, ограниченная кривой y = f (x) и прямыми y=0, х=а и х= b , вращается вокруг оси Ох, тогда объем тела вращения вычисляется по формуле
6. Пусть криволинейная трапеция, ограниченная кривой х= g (y) и
прямыми x =0, y = c и y = d , вращается вокруг оси О y , тогда объем тела вращения вычисляется по формуле
7. Если плоская кривая отнесена к прямоугольной системе координат и задана уравнением y = f (x) (или x = F (y)), то длина дуги определяется формулой
Лекция 18. Приложения определенного интеграла.
18.1. Вычисление площадей плоских фигур.
Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.
Для нахождения суммарной площади используется формула .
Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.
Пример. Найти площадь фигуры, ограниченной линиями y = x, y = x 2 , x = 2.

Искомая площадь (заштрихована на рисунке) может быть найдена по формуле:
18.2. Нахождение площади криволинейного сектора.
Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид = f(), где - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а - угол наклона этого радиус – вектора к полярной оси.
Площадь криволинейного сектора может быть найдена по формуле

18.3. Вычисление длины дуги кривой.
 y y = f(x)
y y = f(x)
S i y i
Длина ломаной линии, которая соответствует дуге, может быть найдена как  .
.
Тогда длина дуги равна  .
.
Из геометрических соображений: 
В то же время 
Тогда можно показать, что

Т.е. 
Если уравнение кривой задано параметрически, то с учетом правил вычисления производной параметрически заданной, получаем
 ,
,
где х = (t) и у = (t).
Если задана пространственная кривая , и х = (t), у = (t) и z = Z(t), то

Если кривая задана в полярных координатах , то
 , = f().
, = f().
Пример: Найти длину окружности, заданной уравнением x 2 + y 2 = r 2 .
1 способ.
Выразим из уравнения переменную у. 
Найдем производную 
Тогда S = 2r. Получили общеизвестную формулу длины окружности.
2 способ.
Если представить заданное уравнение в полярной системе координат, то получим: r 2 cos 2 + r 2 sin 2 = r 2 , т.е. функция = f() = r,  тогда
тогда

18.4. Вычисление объемов тел.
Вычисление объема тела по известным площадям его параллельных сечений.
Пусть имеется тело объема V. Площадь любого поперечного сечения тела Q, известна как непрерывная функция Q = Q(x). Разобьем тело на “слои” поперечными сечениями, проходящими через точки х i разбиения отрезка . Т.к. на каком- либо промежуточном отрезке разбиения функция Q(x) непрерывна, то принимает на нем наибольшее и наименьшее значения. Обозначим их соответственно M i и m i .
Если на этих наибольшем и наименьшем сечениях построить цилиндры с образующими, параллельными оси х, то объемы этих цилиндров будут соответственно равны M i x i и m i x i здесь x i = x i - x i -1 .
Произведя такие построения для всех отрезков разбиения, получим цилиндры, объемы которых равны соответственно  и
и  .
.
При стремлении к нулю шага разбиения , эти суммы имеют общий предел:

Таким образом, объем тела может быть найден по формуле:

Недостатком этой формулы является то, что для нахождения объема необходимо знать функцию Q(x), что весьма проблематично для сложных тел.
Пример: Найти объем шара радиуса R.
В поперечных сечениях шара получаются окружности переменного радиуса у. В зависимости от текущей координаты х этот радиус выражается по формуле  .
.
Тогда функция площадей сечений имеет вид: Q(x) =  .
.
Получаем объем шара:
Пример: Найти объем произвольной пирамиды с высотой Н и площадью основания S.
При пересечении пирамиды плоскостями, перпендикулярными высоте, в сечении получаем фигуры, подобные основанию. Коэффициент подобия этих фигур равен отношению x/H, где х – расстояние от плоскости сечения до вершины пирамиды.
Из геометрии известно, что отношение площадей подобных фигур равно коэффициенту подобия в квадрате, т.е.
Отсюда получаем функцию площадей сечений: 
Находим объем пирамиды: 
18.5. Объем тел вращения.
Рассмотрим кривую, заданную уравнением y = f(x). Предположим, что функция f(x) непрерывна на отрезке . Если соответствующую ей криволинейную трапецию с основаниями а и b вращать вокруг оси Ох, то получим так называемое тело вращения .
 y = f(x)
y = f(x)
Т.к. каждое сечение тела плоскостью x = const представляет собой круг радиуса  , то объем тела вращения может быть легко найден по полученной выше формуле:
, то объем тела вращения может быть легко найден по полученной выше формуле:

18.6. Площадь поверхности тела вращения.
 М i B
М i B
Определение: Площадью поверхности вращения кривой АВ вокруг данной оси называют предел, к которому стремятся площади поверхностей вращения ломаных, вписанных в кривую АВ, при стремлении к нулю наибольших из длин звеньев этих ломаных.
Разобьем дугу АВ на n частей точками M 0 , M 1 , M 2 , … , M n . Координаты вершин полученной ломаной имеют координаты x i и y i . При вращении ломаной вокруг оси получим поверхность, состоящую из боковых поверхностей усеченных конусов, площадь которых равна P i . Эта площадь может быть найдена по формуле:

Здесь S i – длина каждой хорды.

Применяем теорему Лагранжа (см. Теорема Лагранжа
) к отношению  .
.